Assume magnetic field oscillating at fM = 5 Hz with rms amplitude B0, and a Hall sensor measuring the magnetic field at fH = 23 Hz with a rms current I0. Both current I and voltage V are measured with the system.
The magnetic field is
B(t) = √2 * B0 * sin(2πfMt),
the current
I(t) = √2 * I0*sin(2πfHt).
Then the Hall voltage becomes
V(t) = RH * B(t) * I(t)
= 2RH * B0 * I0 * sin(2πfMt) * sin(2πfHt)
= RH * B0 * I0 * {cos[2π(fH–fM)t] – cos[2π(fH+fM)t]}.
By measuring the current at frequency fH and the Y-component of the voltage at fH–fM or fH+fM both I0 and B0 can be calculated.
The sum or difference of two arbitrary frequencies can be set for frequency 8. Both internally generated frequencies as well as PLL frequencies can be used.
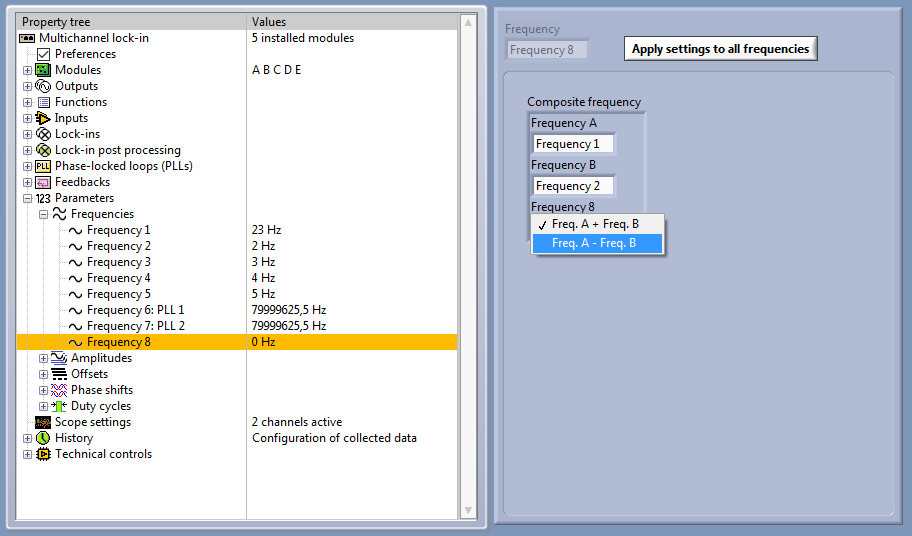
Alternatively, if both frequencies have a greatest common divisor, a base frequency can be set to the greatest common divisor, and the frequencies can be selected as higher harmonics in the multiple harmonics mode.