The MCL1-540 uses two filters: a synchronous filter, and a two stage exponential low pass filter. The time constants of all filters texp,1 texp,2 and tsync can be set individually, and the exponential filters can be disabled.
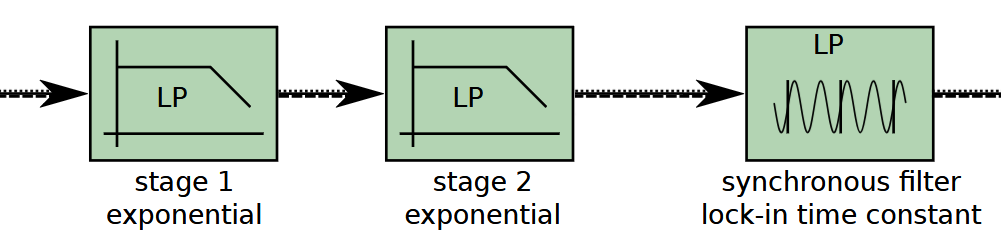
The synchronous filter is always active and controlled by the main time constant and set frequency, as the main filter.
The exact filter time constant is given by the number of cycles q for each sample times the frequency of that sample, tsync,exact=q/f, where q is an integer number ≥1. This means a time constant shorter than 1/f is always prolonged to one period. A mismatch of the frequency and time constant will result in alternating time constant to match an integer number q: As the lock-in is internally working in phase space with the frequency being converted into a phase step, a sample is taken once tsync has passed since the the last tsync had passed, and the phase reaches 2π.
The synchronous filter is a kind of FIR filter. As such it ensures that each datapoint is independent (as long as any low-pass filters are not used). The filter characteristics also makes it very useful to filter away harmonics without any need for excessive (any) exponential low pass filters.
This synchronous filter gives notches at all frequencies separated from f by 1/tsync,exact.
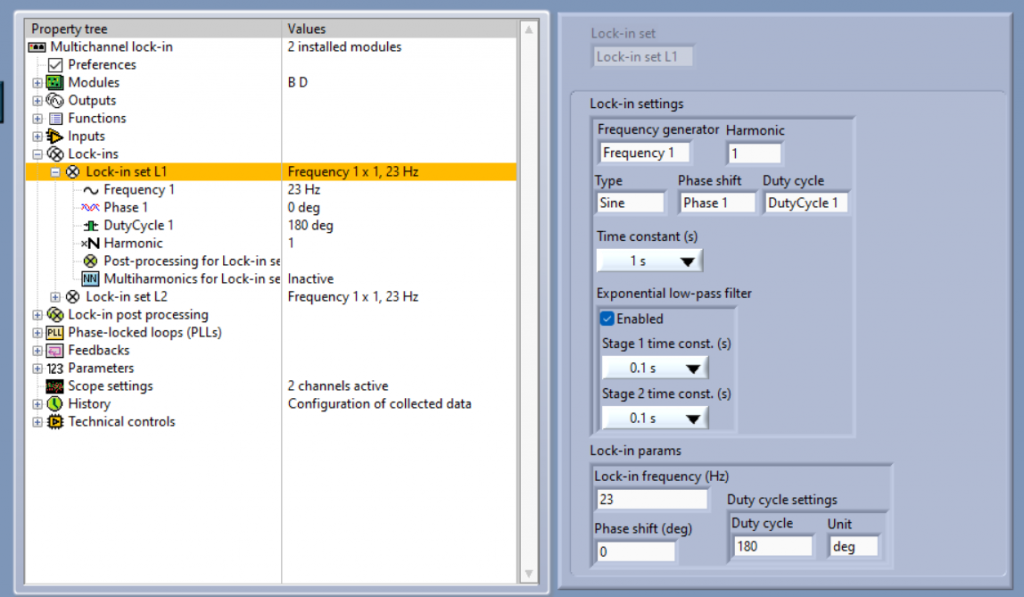
In addition, the exponential low-pass filters can be enabled. They are applied before the synchronous filter. For normal use, we recommend to use the sampling time constant as the longest time, and the exponential low pass filters at least 3-10 times faster or so to yield independent data points. In an environment with only white noise, it is enough to use the synchronous filter without any low-pass filters to give a stable signal with only white noise.
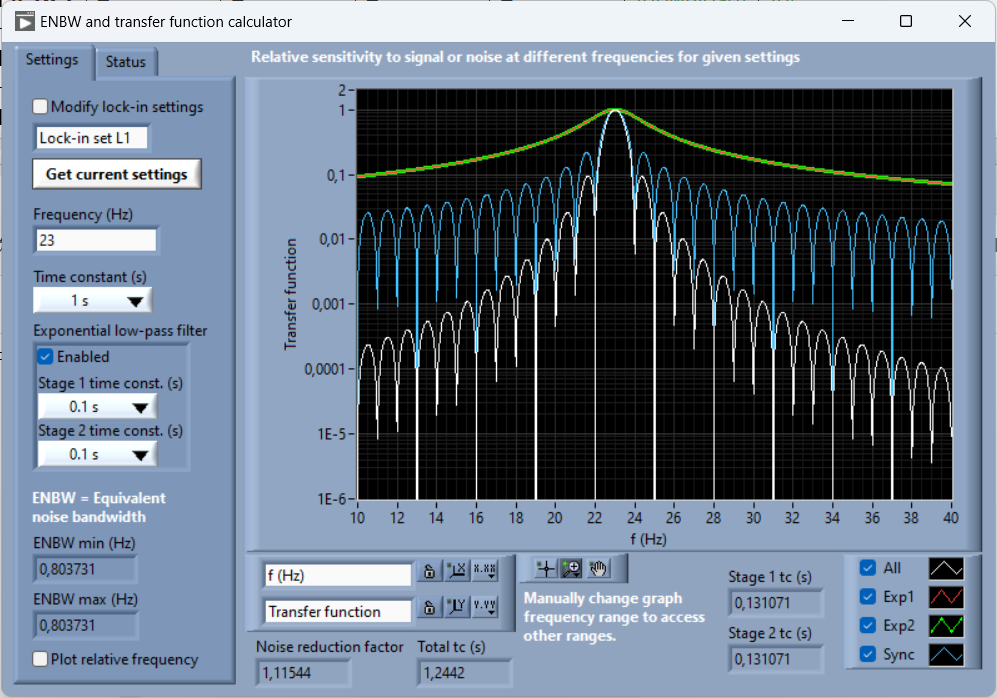
The ENBW tool calculates and integrates the net transfer function for the entire setup, it can be found on the downloads page.